The Bandai Pippin? Yeah, it runs Quake.
… with caveats. 😉
It doesn’t run well, but it does run. This is the 1997 Lion Entertainment port, version 1.08.4, published by MacSoft. I’ve observed that 1.09 breaks sound, and 1.08.5 is unobtainium as of the time of this writing, so 1.08.4 it is. And it’s playable. 🙂
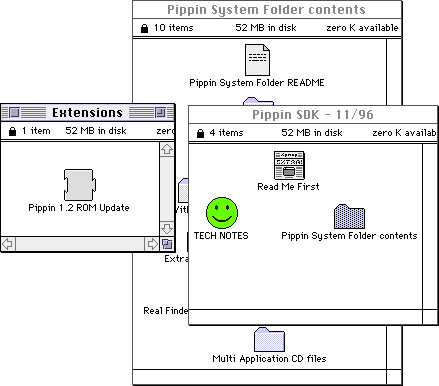
Right out of the box, it’s not playable without first setting up a proper configuration of Pippin OS from which to boot. The minimum System Folder provided with the Pippin SDK is, well, minimal, including only a patch for units with ROM 1.2:
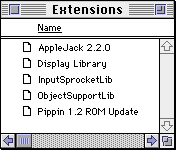
By itself, this won’t do to get Quake working, since Quake won’t launch at all without its required support libraries. Of course we’ll want to play using a Pippin controller, but we’ll want to do so on as small a RAM budget as we can. Through some trial and error, I determined the minimal set of extensions necessary to make satisfy these conditions:
This omits Open Transport and/or IPX for networking, but is good enough for starters, and Quake will simply disable networking if those libraries aren’t present. The rest are required though:
- Display Library is built into System 7.5.3 and later, and into versions of Apple’s Display Enabler starting with 2.3.4 (from Apple Display Software 1.6). Since Pippin OS is based on System 7.5.2, we need to supply this library ourselves (version 1.0b1). Display Library is what enables System 7.5 to switch screen resolutions on the fly. Pippin has only one fixed screen resolution—640×480—so while we won’t be utilizing the Display Library, Quake links to it, so it needs to be present. Without it, Quake puts up this alert at launch:
- ObjectSupportLib is built into Mac OS 8 and later, but needs to be supplied for System 7 to support Apple Event objects used by AppleScript—we’re providing version 1.0.2 here from System 7.5.2. In addition to the required suite of ‘open’, ‘print’, ‘quit’, and ‘run’ corresponding to the
odoc,pdoc,quit, andoappApple Events respectively, Quake supports a “Quake Suite” of one event: ‘console.’ It is possible to utilize AppleScript to issue automated console commands to Quake while it’s running (cool!), but even though we won’t be doing that on Pippin, this library must exist to support that feature. Without it, Quake puts up this alert at launch: - InputSprocketLib 1.2 is part of Apple’s Game Sprockets collection from April 1997. It provides a common interface to any of a collection of input device drivers, the latter of which are installed alongside and “plug in” to InputSprocket itself. Quake links to InputSprocketLib so that it can support input devices other than mouse and keyboard. Without it, Quake puts up this alert at launch:

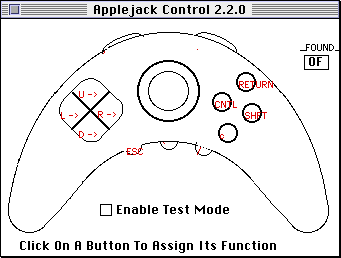
Seeing a pattern yet? - AppleJack 2.2.0 is an extension provided with the last version of the Pippin SDK from November 1996. It allows a Pippin controller—informally called an “AppleJack”—to emulate a keyboard by mapping its 13 buttons to any combination of keys and modifiers, ignoring the trackball. The AppleJack extension comes with an application called “AJ Control” which is used to configure the aforementioned desired mappings. AJ Control’s results can be applied globally (the default) or saved as a ‘pipp’ resource to be injected into applications where particular configurations are needed per-application. The AppleJack extension is smart enough to detect a ‘pipp’ resource in the active resource fork, and then activates the configuration saved therein on the fly, overriding the global settings.
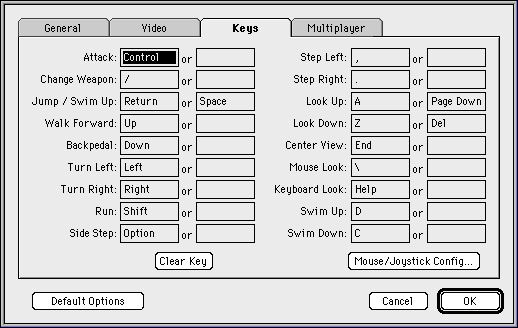
I configured the AppleJack extension with a global mapping to Quake’s default keyboard bindings, since I don’t want to mess with the Quake application itself and because my “Pippinized” Quake CD doesn’t play anything other than Quake. Astute readers may notice that my list of extensions above omits any InputSprocket drivers. Why am I emulating the keyboard and mouse, rather than using InputSprocket? I discovered that the Mac version of Quake has some unfortunate quirks with its input handling that make using InputSprocket difficult on Pippin, notably that InputSprocket completely takes control of an input device when active, and Quake’s InputSprocket bindings only apply to in-game actions. The Mac version of Quake unfortunately provides no InputSprocket bindings for using the menus; a keyboard and mouse are required for those. Without a way to select menu options, it is impossible to start a new game. By installing InputSprocket without any drivers, when it searches for devices it knows how to take over, it will find none, yet Quake’s requirement for the InputSprocket library will be satisfied.
Quake doesn’t use InputSprocket for the keyboard, but Quake does use InputSprocket exclusively for binding mouse movement and button clicks. Unfortunately yet again, even though the trackball on a Pippin controller emulates a mouse, InputSprocket will not see a Pippin controller as anything other than what it actually is: a Pippin/AppleJack controller (even on a Power Mac, naturally lacking a Pippin controller driver in ROM). Allowing InputSprocket to handle a controller for mouse movement again precludes us from using it as an emulated keyboard. We’re stuck between a rock and a hard place: either we let InputSprocket take command but give up the ability to use menus (therefore requiring a keyboard to also be attached), or we emulate a keyboard with the AppleJack extension and give up the Pippin controller’s trackball. I opted for the latter; Quake did not originally ship with mouselook enabled by default, so it should be playable without it. So close, though—maybe a future source port of Quake can rectify this discrepancy? 😉
I chose a button mapping similar to that used by Super Marathon:
- D-pad: Move/Turn
- Left trigger: Step Left
- Right trigger: Step Right
- Red: Look
- Green: Action
- Yellow: Trigger
- Blue: 2nd Trigger
- Square: Quit
- Circle: Auto Map
- Diamond: Next Weapon
Quake doesn’t have an action button nor an alternate fire, so I repurposed those buttons for other useful functions:
- D-pad: Move/Turn (Arrow keys)
- Left trigger: Step Left
- Right trigger: Step Right
- Red: Swim Down
- Green: Run
- Yellow: Attack
- Blue: Jump / Swim Up (Return key)
- Square: Menu (Esc)
- Circle: Console
- Diamond: Change Weapon
Pippin’s video chip, called “Taos,” shares its memory and data bus with the PowerPC 603 CPU. This bus is 32 bits wide, which means Pippin can read from or write to memory up to 32 bits at a time. A byte-sized (8-bit) write to video memory takes the same amount of time as a halfword-sized (16-bit) write or a word-sized (32-bit) write: 8 cycles. When making smaller writes, the unused bits in that 32-bit-wide “channel” are simply ignored, and therefore wasted. To maximize the available bandwidth, in 8-bit color mode, two or four pixels can be written to the screen in the same amount of time it takes to write a single pixel. Instead of writing just one colored pixel to Pippin’s linear chunky framebuffer, it costs exactly the same to write two adjacent pixels of the same color. Taking advantage of this, games like Quake can offer horizontal pixel doubling for free on Pippin, with no performance penalty.
It’s a lot like making ice. You can make one ice cube by freezing a tray with just one compartment filled, or you can make an entire tray of ice by filling the whole tray. Either way, the water takes the same amount of time to freeze. It is therefore the most time-efficient to fill as much of the tray at once.

In addition to doubling Quake’s horizontal resolution from 320 pixels to the full screen width of 640 pixels, the vertical dimension can be extended as well. However, unlike in the horizontal direction, scaling rendered frames from 240 lines to 480 lines comes at a performance cost which is preferably avoided. Instead, I only render every other scanline, leaving the rest blank and taking advantage of the fact that the screen need not be cleared every frame to accommodate this. When hooked up to a display via Pippin’s composite video output, the effect of line skipping is much less pronounced versus in an RGB/VGA mode; Taos’s hardware scaling and convolution “blurs” the scanlines together resulting in a continuous image. The tradeoff is that the image appears darker overall. I compensate for this by cranking up the game brightness as far as it will go. (There is a more scientific way to determine the best brightness scale value, involving gamma correction math, but I just eyeballed it based on what I thought looks good.)



As a final cherry on top, even though Quake’s official minimum requirements call for 16 megabytes of RAM, that’s not entirely accurate. 😉
I suspect Lion Entertainment determined early on that eight megabytes is insufficient, and then only tested at or above 16MB configurations, thereby arriving at the indicated minimum spec. But to Lion’s credit, the Mac version of Quake is flexible with regards to available memory and will not simply quit if there is not at least 16MB installed in the system. It needs a heap of at least 5.3 megabytes in size or it will gracefully refuse to start. It apparently sets aside at least 1.8 megabytes of additional overhead for itself, so if the Quake application is allocated 7100K, it will still run safely, despite Finder’s warnings that it may crash. The smaller Quake’s heap, the more often it has to read from disk resulting in performance hitches during gameplay, so of course it is advantageous to allocate Quake as much RAM as possible. System 7.5 uses at least two megabytes for itself, so clearly Quake cannot run on an 8MB system, but it can squeeze into a 12MB configuration such as a base model PowerBook 1400cs. When equipped with an 8MB memory module, a Pippin has 13MB of RAM available, of which up to 11MB can be provided to an application. 7100K easily fits within those parameters, which means that even Pippins equipped with somewhat common 8MB modules can enjoy Quake. 🙂
Enough about getting it working. Now that it runs, let’s see some timedemo benchmarks! Running with nosound 1, we get:
5.5 FPS is… not great, but also not bad considering Quake itself was released several months after the Pippin Atmark and targeted a fairly high-end (for the time) Pentium PC. I’ve certainly played on worse. Quake’s performance on Pippin to me is reminiscent of Quake running on a 486/66, which coincidentally shares the same clock speed as a Pippin Atmark. While I wouldn’t expect to score any frags in a serious deathmatch with this setup, it is still impressive that Quake runs as well as it does on Pippin hardware, absent any hardware acceleration. If Quake can look this good on a CRT when scaled to full screen, I have high expectations for less technically-demanding games as examples of how Pippin can shine.